Introduction

Basics

One of man's earliest reasons for attempting to understand the motions of the sun, moon, and planets was his belief that they controlled his destiny. Other reasons were his need to measure time and later to use the celestial objects for navigation.
In 1601, Johann Kepler (1571-1630) became the director of the Prague Observatory on the death of Tycho Brahe (1546-1601), who had observed for 13 years the relative motion of the planet Mars. By 1609, Kepler had formulated his first two laws and, in 1619, published the third law, which he dedicated to James I of England. Kepler stated that:

1. planet moves in an orbit that is an ellipse, with the sun at one focus of the ellipse.
2. The radius vector drawn from the sun to any planet sweeps out equal areas in equal times.
3. The squares of the periods of revolution of the planets are proportional to the cubes of the semimajor axes of their orbits.

Years later, the following three laws of motion given by Newton became the axioms of mechanics:

1. Every particle persists in a state of rest or of uniform motion in a straight line (i.e., with constant velocity) unless acted on by a force.
2. If F is the (external) force acting on a particle of mass m which, as a consequence, is moving with velocity v, then:

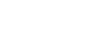
Where p = mv is called the momentum. If m is independent of time t, this becomes:

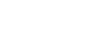
Where a is the acceleration of the particle.
3. If particle 1 acts on particle 2 with a force F12 in a direction along the line joining the particles while particle 2 acts on particle 1 with a force F21, then F21=F12. In other words, to every action there is an equal and opposite reaction.

Orbital Mechanics

By considering the motion of a spacecraft around an astronomical body (Planet), Newton's second law can be stated in the form:

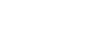
Where is the position vector from the center of attraction to the spacecraft and 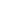the gravitational parameter of the astronomical body with the unit of km³/s². Since the position vector is in the plane defined by the center of attraction and the acceleration vector, it is evident that the motion is in a plane through the center of attraction.
Solving the above equation yields the orbit equation:

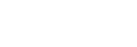
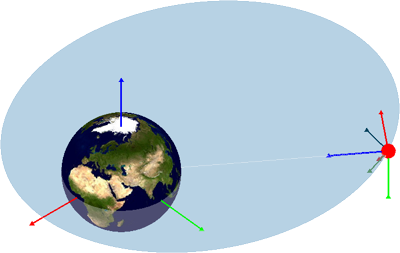
Where h is the relative angular momentum of spacecraft, that is, the specific relative angular momentum .The unit of h is km²/s. e is the eccentricity (the magnitude of the eccentricity vector 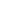) and is the true anomaly which is the angle between the fixed vector and the variable position vector as illustrated below:

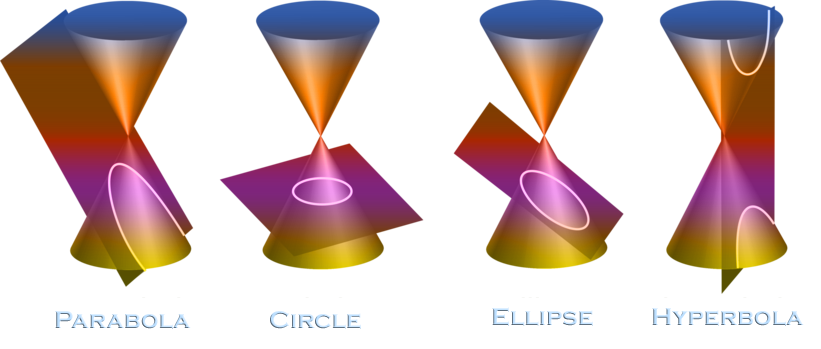
The orbit equation shows that the path of one of the masses relative to the other is a conic section (circle, ellipse, parabola, or hyperbola) whose shape is determined by the eccentricity.

Simplifying Newton's second law of motion also yields:

Or:

Where is a constant. v²/2 Is the relative kinetic energy per unit mass. 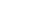is the potential energy per unit mass of the body m₂ in the gravitational field of m₁. The total mechanical energy per unit mass is the sum of the kinetic and potential energies per unit mass. The above equation is a statement of the conservation of energy, namely, that the specific mechanical energy is the same at all points of the trajectory. This equation is also known as the vis-viva (living force) equation. It is valid for any trajectory, including rectilinear ones.

Circular Orbits

Elliptical Orbits

Parabolic Orbits

Hyperbolic Orbits

Orbital Parameters

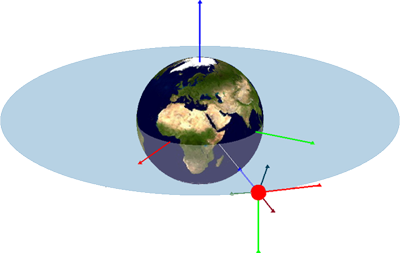
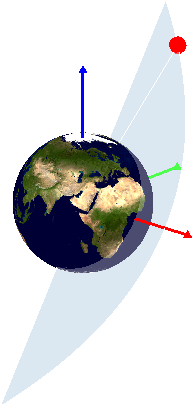
To define an orbit in the plane requires two parameters: eccentricity and angular momentum. Other parameters, such as the semimajor axis, the specific energy, and (for an ellipse) the period are obtained from these two. To locate a point on the orbit requires a third parameter, the true anomaly, which leads us to the time since perigee. Describing the orientation of an orbit in three dimensions requires three additional parameters, called the Euler angles, which are illustrated below.

The angle i between the orbital plane and the Earth’s equatorial plane is known as the orbital inclination. Inclination is measured at the intersection of the Earth’s equatorial plane with the orbital plane at the point where the spacecraft crosses the equator from south to north. The line formed by the intersection of the two planes where the satellite passes from the southern to northern hemisphere is called the line of ascending nodes. The orbital inclination is also equal to the angle between the K unit vector in inertial frame and the h (angular momentum) vector in the perifocal coordinate system.
The numerical value of i ranges between 0^o and 180^o. At first glance, this may seem to exclude a whole set of orbits. However, the direction of motion of the satellite about the Earth has not been considered. If the satellites motion is from west to east, the orbit is referred to as a direct orbit. If the motion is from east to west, then the orbit is said to be retrograde. Once the type of orbit (direct or retrograde) is specified, then i needs only to take on values in the range indicated above.
There are two other angles, the longitude of the ascending node and the argument of perigee, which are classical orbital elements. These angles are defined by the geometric relationship between the inertial frame and perifocal systems. The longitude of the ascending node, , is the angle measured in the equatorial plane from X axis to the line of the ascending node. The argument of perigee is the angle measured in the orbital plane between the line of the ascending node and the perifocus. Both angles range in value from 0^o to 360^o.

In summary, the six orbital elements are:

1. a: semi-major axis (or alternatively h: specific angular momentum)
2. i: inclination
3. : right ascension (RA) of the ascending node
4. e: eccentricity
5. : argument of perigee
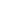6. : true anomaly

Thus far, three of the six classical orbital elements have been identified. The three angles, i, and define the orbital plane’s spatial orientation with respect to the IJK coordinates. They do not provide any information about the shape of the orbit or the length of the semimajor axis. Thus, the semimajor axis and the eccentricity are included as classical orbital elements. The sixth orbital element is an epoch (true anomaly 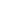), or benchmark time T₀ when the angles i, and were measured.
The angles i, and also provide a means of transforming coordinates between the IJK and perifocal systems.
There are times when an inertial coordinate system such as the perifocal system makes a calculation or analysis more difficult than the use of a noninertial system. For example, updating the orbital position of a satellite is much more easily accomplished in a coordinate system that rotates with the satellite as it moves around the Earth.

References

• Curtis, H. (2010). Orbital mechanics for engineering students. 2st ed. Oxford: Elsevier Butterworth-Heinemann
• Chobotov, V. (2002). Orbital mechanics. 1st ed. Reston, Va.: American Institute of Aeronautics and Astronautics
• Sidi, M. (1997). Spacecraft dynamics and control. 1st ed. Cambridge: Cambridge University Press
• Madonna, R. (1997). Orbital mechanics. 1st ed. Malabar, Fla.: Krieger Pub. Co
• Prussing, J. and Conway, B. (1993). Orbital mechanics. 1st ed. New York: Oxford University Press
• Bate, R., Mueller, D. and White, J., (1971). Fundamentals of astrodynamics. 1st ed. New York: Dover Publications